Probability P
확률이란, 어떤 Event가 일어날 수 있는 가능성을 뜻한다.
특징으로는, 확률은 0과 1사이의 값을 가지며, 확률 전체의 합은 1이 된다.
1. Random Variable (확률변수)
Def:
확률 공간(Probability Space : Ω, F, P)가 주어졌을 때, 표본 공간(Sample Space: Ω) 의 대상 공간(Target Space : T)을 내가 관심있는 특정한 양이라고 한다면, 함수 X: Ω → T 를 확률변수라고 한다.
Example:
Ω = {(H,H), (H,T), (T,H), (T,T)} (표본공간): random experiment에서 나올 수 있는 모든 경우의 수들의 집합
X((T,H)) = 1, X((T,T)) = 0 : 확률변수 X를 H가 나오는 갯수라고 정의한다면, 이 식이 만족된다.
P(X = 2) = P((H,H)) = ... : X가 2가 될 '확률'로 P notation을 사용했다.
즉, 확률변수는 함수이기 때문에 값으로 변환된다는 것을 명심해야 한다. 확률변수의 가장 중요한 점으로는,확률변수 또한 분포(distribution)을 가지고 있다는 점이다. 그래서 후에 통계공부를 하다보면 확률분포와 같은 Term이 나오는데, 이 확률변수의 분포를 뜻한다.
확률변수는 이산형(Discrete)와 연속형(Continuous)으로 나뉜다.

이산형과 연속형 각각 유명한 분포들을 기본적으로는 알고 있으면 좋다.
2. Discrete Distribution (이산형 분포)
2.1 Binomial Distribution (이항분포)
연관된 분포: Bernoulli 분포(가장 기본), 음이항분포
우선 베르누이 분포부터 알아보아야 한다. (가장 기초!)
어떤 시행의 결과가 성공/실패 (딱 두개)일 때, 성공할 확률을 p라고 한다. 그러면 확률분포는... (so easy..)

자 이제 이항분포다. 베르누이 확률변수 X 가 iid하다고 가정한다면, 이들의 합인 Y는 이항분포를 따른다.

여기서 nCy 나올 수 있는 모든 가짓수의 콤비네이션이라는거...!번외로, 음이항분포라고 성공까지의 실패횟수를 나타내는 분포도 있다. 음이항분포는 기하분포의 일반화 버전이기에 기하분포에서 다뤄볼 것이다.
2.2 Poisson Distribution (포아송 분포)
연관된 분포: 이항분포(np=lambda 에서 n이 무한이면 포아송에 근사.. 이걸로 이항분포의 n의 값이 크면 포아송으로 풀기 쉬워진다.)
포아송도 정말 잘 쓰는 확률분포 중 하나이다. 포아송은 lambda라는 모수가 존재한다 :> (모수는 보통 funtion에서 세미콜론 뒤에 적어두면 편함)


Figure 2.2.1을 참고하면, 여기서 람다는 단위시간 내에 어떤 사건이 평균적으로 일어날 횟수(보통 주어짐), X는 그 사건이 일어날 횟수를 뜻한다.
예를 들어 한 콜센터에서는 1분에 평균적으로 5.2건의 콜이 들어온다고 하자, 그러면 1분에 1건 이하의 콜이 들어올 확률을 구하자고 하면,단위시간(1분)에 5.2건이니 람다=5.2를 대입하면 된다.
X는 사건이 일어날 횟수기 때문에, X=0,1 (1건 이하기 때문)의 경우를 전부 더해줘야 한다. 즉, P(X=0;람다=5.2)+P(X=1;람다=5.2)를 더하면 확률이 나온다. n이 많은 경우, 특히 리스크 관련해서 몇천건 당의 확률로 가면 이항분포를 포아송으로 근사하여 계산하면 된다.
2.3 Geometric Distribution (기하분포)
연관된 분포: Hypergeometric 분포
기하분포는 성공하기까지의 실패횟수를 확률변수로 두고있다.

식으로 보면 훨씬 쉽다. 말 그대로 성공할 때까지(성공확률: p)의 실패횟수임을 확률질량함수를 통해 직관적으로 알 수 있다.
기하분포의 특징으로는 지수분포와 같게 무기억성의 특징이 있는데, 식으로 설명하자면
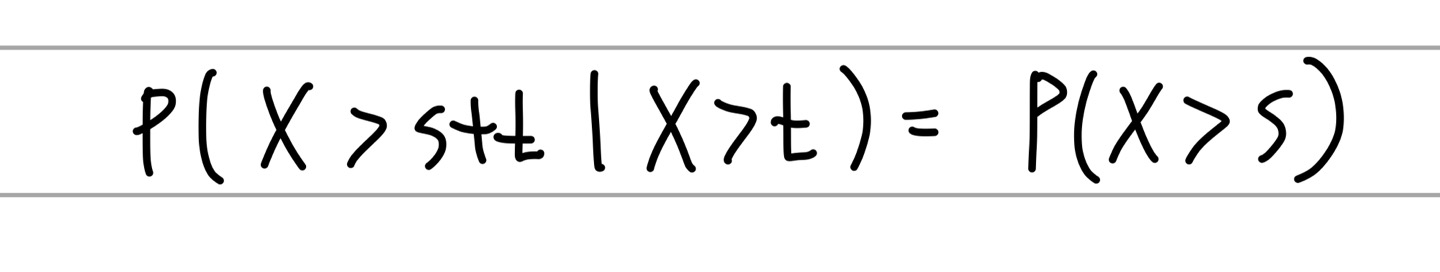
t를 조건부로 달아도 s는 영향을 받지 않는다는 것을 알 수 있다. 여기서 s 와 t 는 시점을 (시계열 생각하면 쉽다) 나타내는데, 교재에서는 쉽게 기계의 고장에 빗대서 설명한다. t 시점에서 기계가 고장나지 않았다고해서 t+s 시점에 영향을 주는 것이 없고, t+s 시점이나 s시점이나 기계가 고장날 확률은 같다는 것이다.
2.4 Negative binomial Distribution (음이항분포)
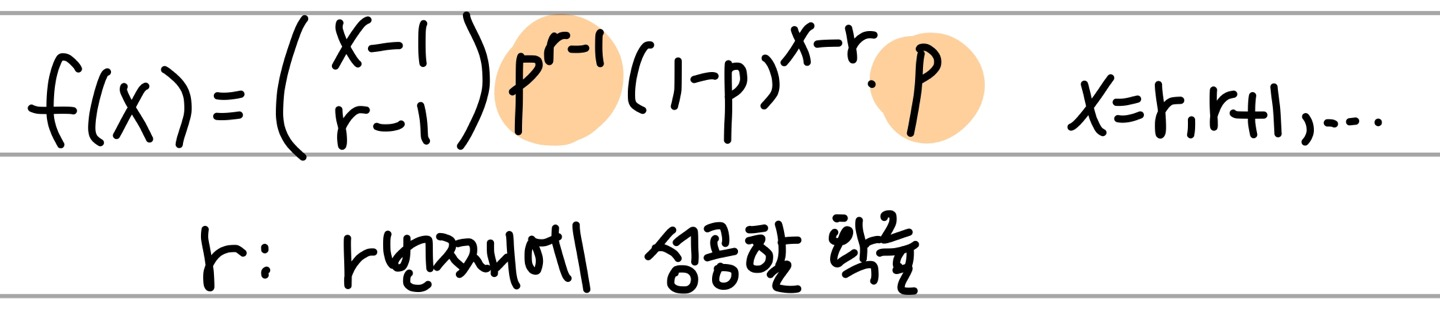
이항분포와 매우 같다~ 여기서 X는 r번째에 성공할 때까지 걸리는 실패 횟수다...

조합의 성질을 이용하여 조작하면, x = 0,1,2 범위로 바꿀 수 있다.
2.5 Hypergeometric Distribution (초기하분포)
연관된 분포: 음이항분포
음이항분포는 복원추출, 초기하분포는 비복원추출인 것이 서로 다른 점이다.

이것도 조합식이다.... N가 쉽게 얘기해서 M(내가 원하는 집단 ex.파란 공, 불량품...)이 섞여있는 전체 모집단이고, 내가 여기서 n개의 샘플을 뽑았을 때, M에 속한 x개와 N-M에 속한 n-x가 나올 확률..... 이다 주로 품질에서 나옴
3. Continuous Distribution (연속형 분포)
3.1 Uniform distribution (균일분포)
이 친구는 아주 간단쓰하다. 이산형 분포들은 모수(람다나, 확률p나, M이나.. )에 따라 분포들이 휙휙 바뀌는데, 연속형은 나아름 모양을 유지한다 ㅠㅠ

균일분포는 (0,1) 사이에 있으면 indicator ftn으로도 사용되는데, 이게 파티셔닝할 때나 표기할 때 엄청 편해서 익숙해지면 좋다.
3.2 Normal Distribution (정규분포)
연관된 분포: 카이스퀘어분포, T분포, F분포
세상에서 통계를 배울 때 가장 중요한 분포라고 할 수 있는 정규분포가 나왔다.

정규분포는 대칭이며, 파라미터가 뮤랑 시그마로 두개가 존재한다. 옆에 그림이 두 개의 파라미터를 잘 설명했다.(아마도)
통계에서 배우는 중요한 Theorem인 중심극한정리의 중심에는 이 분포가 있다.
중심극한정리 (Central Limit Theorem)란,

이거 한마디로 끝난다. 우리가 한 모분포에서 iid하게 뽑은 표본집단들의 크기가 커질수록, 그 표본평균이 무려 정규분포로 근사한다는 뜻이다. 우리가 모르는 분포를 정규분포로 가정할 수 있는 핵심 키가 되고, 이걸로 실제로 많은 문제들을 쉽게 풀수있다.... 확장판으로 뭐 델타법칙 이런게 있지만 시간이 있으면 다뤄보겠다. 이거는 통계학도라면 무조건 외운다기보단 이해하고 남들 앞에서 쉽게 설명이 가능할 정도였으면 좋겠다.
로그정규분포도 가끔 사용되는데, 이는 0과 무한대 사이의 값들을 설명하기 좋기 때문이다.
또한 정규분포에서 파생되는 분포로는, 카이스퀘어분포(감마분포와도 같으면서 표준정규분포의 제곱과도 같은 마법의 분포)와 이 둘을 활용한 F분포, T분포 등등이 있다. 이것도 시간이 나면 다루겠다.ㅠㅠㅠ양이너무많다.
3.3 Exponential Distribution (지수분포)
연관된 분포: 기하분포 (둘 다 무기억성의 특징이 있다.), 포아송 분포
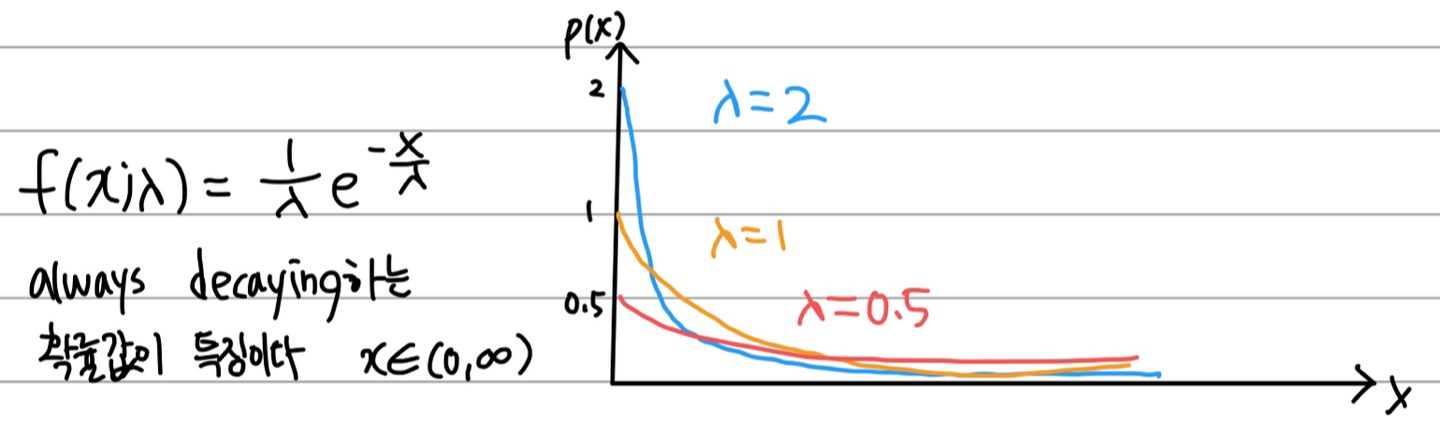
이 친구도 참 많이 다루긴 한다.
지수분포는 특정한 사건이 일어난 후 다시 일어날 때까지 걸리는 시간에 대한 분포다. (포아송이랑 비교해봅시다. 포아송 X: 일어날 횟수)
특정 사건이 많이 발생하면, 당연히 다시 일어날 때까지 걸리는 시간이 짧아지는 것이 저 분포도를 통해 나타난다. 다시 말해서 X 값이 커질수록 확률도 거의 낮아지는 것이 보인다. 하늘색을 보면 가장 먼저 바닥을 치는 것이 보이는데, 이는 사건의 평균적으로 일어날 횟수가 커질수록 그 사건이 또 일어날 때까지 소요시간이 확 짧아지는 것을 나타냅니다.
그 외 베타분포도 있지만 힘들어서 패스.....