본 포스팅은 유사도를 측정하기 위한 아는 모든 개념을 모았다.
간단하게 유사도 계산, 거리, 상관계수가 나온다!
1. Similarity & Dissimilarity
1.1.1 Similarity measure
두 데이터 객체가 어떻게 같은지에 대한 수치적인 계산이다.
두 데이터 객체가 비슷할 수록 높다.
주로 [0,1] 사이의 값이다.
1.1.2 Dissimilarity measure
두 데이터 객체가 어떻게 다른지에 대한 수치적인 계산이다.
두 데이터 객체가 비슷할수록 낮다
최솟값은 주로 0이다
최대 한계값은 다양함. (inf까지 갈 수 있으니 보통 1이라고 한다.)
=> Proximity 는 Similarity나 Dissimilarity를 말할 때 통용되게 쓴다.
1.1.3 Measurement
두 객체 x, y를 하나의 간단한 속성(nominal, ordinal, interval, or ratio)을 가지고있다고 가정하고 similarity와 dissimilarity 계산법을 확인하자.

nominal한 경우는 두 가지가 똑같냐/안똑같냐로 접근하면 되는 것이라 스킵하도록 한다.
ordinal의 경우는 abs(x-y)로 둘 사이의 차이를 계산한 뒤, n-1로 나누어주어 dissimilarity를 구하고, similarity는 1에서 이것을 빼주는 아주 간단한 계산이다.

이에 관련해서는 외국 아티클들에 정보가 별로 없어서 넘어가도록 한다. ㅠㅠ
다음으로 Similarity에 대한 정의와함께 Definition 1번에 반하는 Cosine Similarity, 그리고 Binary Vectors의 Similarity를 짚고 넘어가자.
1.2.1 [Definition] Similarity
1. s(x,y) = 1 (or max similarity) only if x = y (but does not always hold. e.g. cosine)
2. s(x,y) = s(y,x) for all x,y (Symmetry)
where s(x,y) is the similarity between points (data objects), x and y
1.2.2 Cosine Similarity
if $d_1$ and $d_2$ are two document vectors, then
$$cos(d_1,d_2) = {< d_1, d_2 > \over \Vert d_1 \Vert \Vert d_2 \Vert} $$
코사인 유사도는 코사인 각도를 이용해서 구하기 때문에 범위가 [-1, 1]이다. Document Vector은 앞서 Data Processing에서 Bag of Words랑 같다고했다. 이 문서벡터에서 단어들의 유사도를 구할 때 벡터의 방향을 위주로 계산하기 때문에 꽤나 괜찮은 비교법이라고 볼 수 있다. (빈도수에 영향을 받지 않음)
1.2.3 Similarity Between Binary Vectors
보통 x, y 객체가 바이너리 속성만 가지고 있는 경우가 많다.
이 경우 이들의 Similarity를 비교하는 데에 주로 쓰이는 것이 Simple Matching Coef와 Jaccard Coef다.
둘 다 두 객체들의 Similarity를 0과 1사이의 값으로 나타내준다. (맨 위의 개념들을 보면 당연한 것!)
예시를 통해 알아보자.
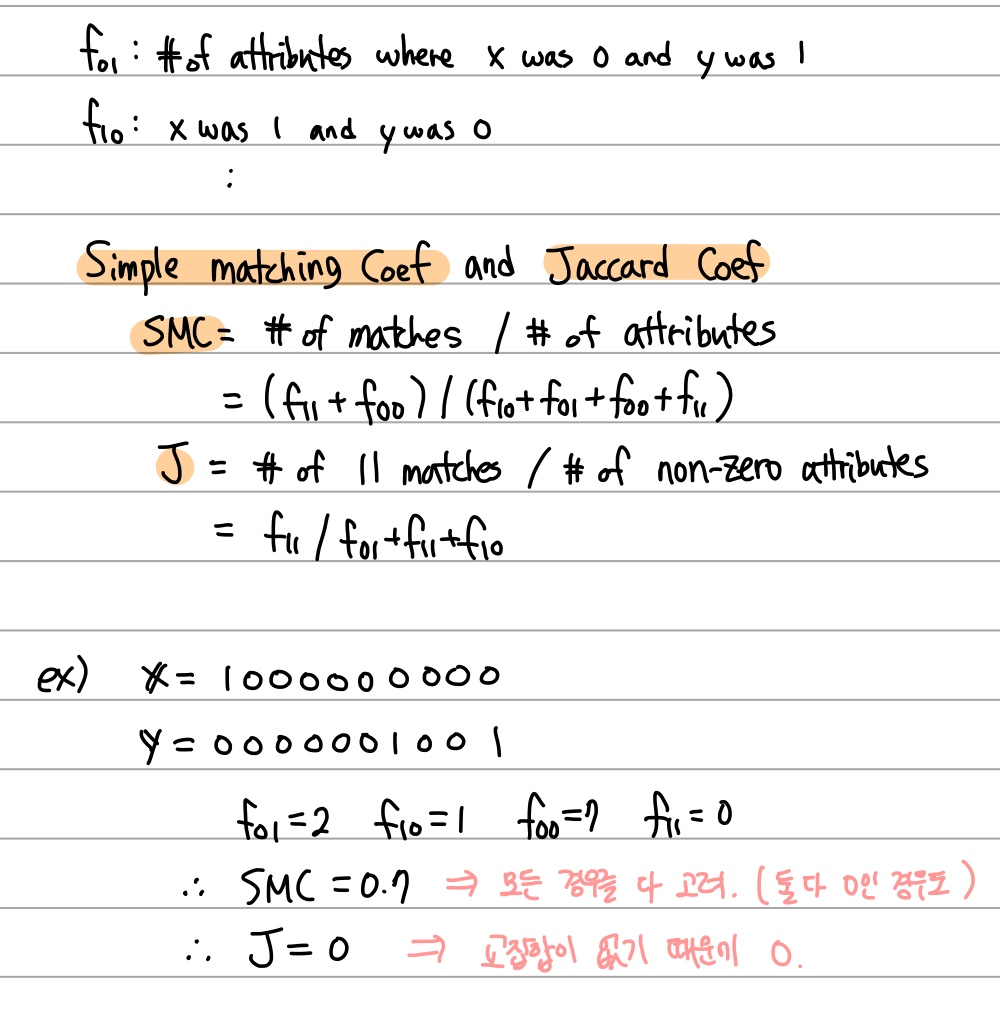
2. Distance
distance는 왜 중요할까? 군집(Clustering)이나 K-means 등 객체 사이의 거리를 이용해서 분석을 하는 알고리즘이 많은 만큼 거리 관련한 개념을 짚고 넘어가야한다.
대표적으로 우리가 알고있는 Euclidean 거리 말고도 Minkowski, Mahalanobis Distance가 있다.
2.1 Euclidean Distance

삼각함수에 기초한 가장 베이직한 거리공식. 스케일이 다르다면 당연히 표준화를 한 뒤에 계산해야한다.
Regularization에서 L1, L2 Norm을 이용하여 가중치를 조절하는데, 유클리디안은 L2에 속한다.
2.2 Minkowski Distance
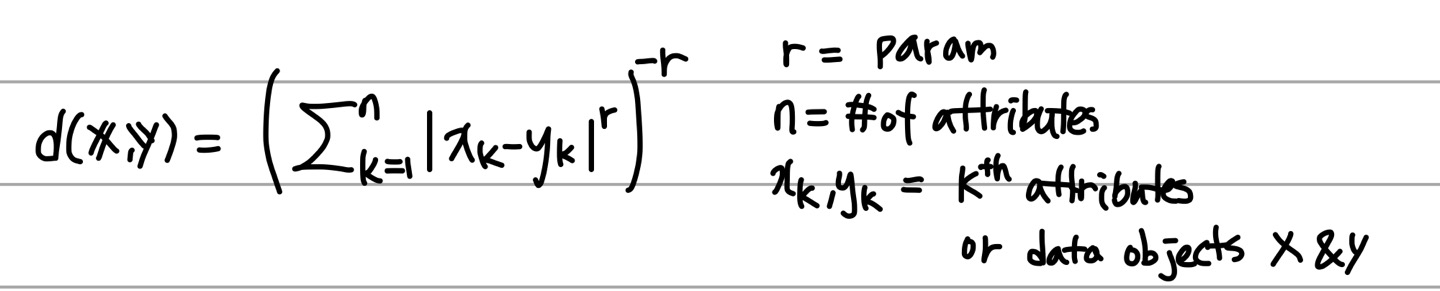
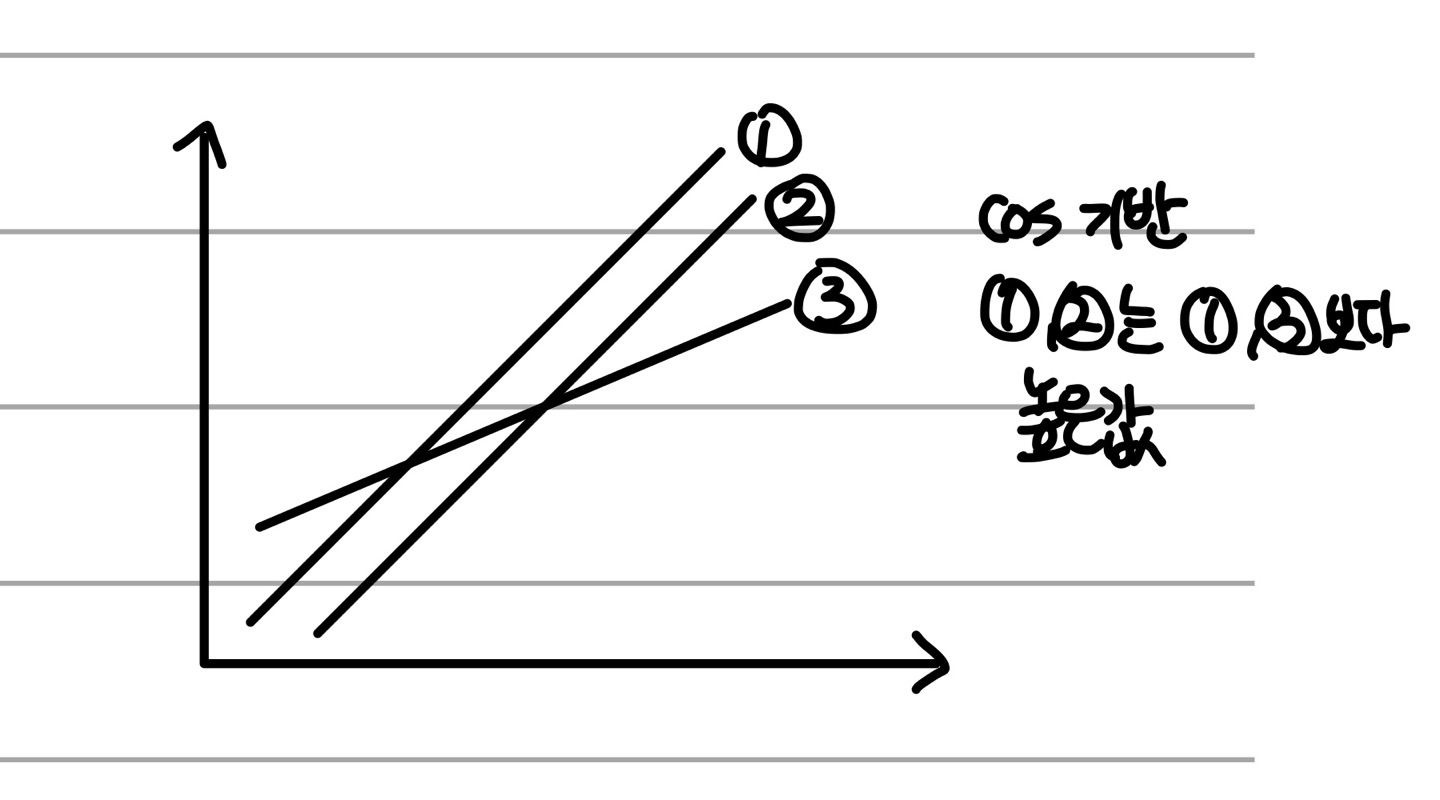
유클리디안 거리의 일반화버전이라고 볼 수 있다.
특징으로는
r = 1일 때 City block Distance (맨하탄 유사도, 택시캡 유사도라고도 한다. L1 norm)
r = 2일 때 유클리디안과 동일, (L2 norm)
r = inf일 때 supremum Distance (L_max norm) 가 있다. 아래 그림은 B 에서 A로 가는 거리를 나타낸 것이다.

2.3 Mahalanobis Distance

이에 관한건 공돌이의 수학정리노트(https://angeloyeo.github.io/2022/09/28/Mahalanobis_distance.html) 에서 설명을 너무 잘해주셨다. 참고해야겠다.
3. Correlation

상관관계란 X와 Y 사이의 선형관계의 정도를 [-1, 1]사이의 수로 나타낸 것으로서, 선형관계의 강도만을 나타낸다는 것을 주의해야한다. 그래서 둘이 Quadratic 관계가 있으면 Correlation은 0으로 계산된다.
상관관계의 좋은점은, Scaling이나 Translation의 변함에 관계없는 값이라는 것이다.
모든 feature에 따라 Similarity를 계산할 때, 하나의 방법으로만 계산하기는 불가능에 가까울 것이다. 그래서 모든 Feature을 기반으로 유사도를 계산하기 위해 Combining Similarity를 하는데, 이는 Indicator Variable을 사용하여 asymmetric한 k번째는 0으로 판단해버리고, 나머지는 1로 계산하여 similarity를 계산할 수 있다.
이렇게 특정한 것을 지우는 것 말고도 가중치(Weights)를 부여해서도 계산할 수 있다.
범주형 자료의 유사성 척도
1) Binary Variable
- Hamming distance
- Jaccard Coefficient(Asymmetric Binary Attributes)
2) Ordinal Variable
3) Nominal Variable
- 전체 10개중에 5개가 일치한다, 5/10만큼 유사하다로 표현이 가능하다.
범주형 자료들에서 유사도를 구하면 KNN의 준비가 됐다.
K = 1; 하나의 가장 근접한 레코드를 사용한다.
K = 5; 5개의 가장 근접한 레코드를 사용한다.
K = n; 전체에서 가장 다수에 속하는 샘플들에 가장 근접한 레코드를 사용한다.
'딥러닝' 카테고리의 다른 글
| 1과목: 데이터 수집 및 저장 계획 (0) | 2023.04.07 |
|---|---|
| [데이터 시각화] 그래프 (0) | 2023.04.01 |
| Information(엔트로피, 상호정보량) (0) | 2023.04.01 |
| 데이터의 품질 (Data Quality) (0) | 2023.04.01 |
| Data Types (0) | 2023.04.01 |